Matrix Inverse Properties
There exists a matrix B such that B A I. The answer to the question shows that.

Solved 3 Which Of The Following Are Properties Of Matrix Chegg Com
Factorization where is a unit upper triangular matrix and D is diagonal.

. Swap the positions of a and d put negatives in front of b and c and divide everything. See examples for calculating the inverse of 2x2 matrices. An inverse matrix is an important tool in mathematics.
A 1 1 A 2Notice that B 1A 1AB. Properties of Matrix Addition. Properties of the Matrix Inverse.
The inverse of a matrix is often used to find the solution of linear equations through the matrix. Bases coordinates and dimension 83 1. The addition of matrices satisfies the.
Matrix properties are useful in many procedures that require two or more matrices. To find the inverse of a 2x2 matrix. Unique inverse exists generalized inverses do Generalized inverses and their uses in solving systems of equations are discussed in Appendix 3 of Lynch Walsh A-is the typical notation.
The following statements are equivalent ie they are either all. The invertible matrix theorem is a theorem in linear algebra which offers a list of equivalent conditions for an nn square matrix A to have an inverse. Three Properties of the Inverse 1If A is a square matrix and B is the inverse of A then A is the inverse of B since AB I BA.
It can be used to solve the bulk of difficult. Learn the inverse matrix definition and explore matrix inverse properties. If A and B are matrices with ABIn then A and B are inverses of each other.
Theorem16 Right Cancellation Law Let A B and C be square matrices of order n. Notice that the order of the matrices has been reversed on the right of the. If Ais non-singular how do we nd A 1.
By using the associative property of matrix multiplication and property of inverse matrix we get B C. Then we have the identity. The inverse of a 2 2 matrix 79 6.
A matrix has to be non singular for it to be invertible ie to have an inverse. If A-1 B then A col k of B ek. The following statements are equivalent.
A square matrix which has a non zero determinant is known as a non singular matrix. Properties of Inverse Matrix and other properties. A matrix for which an inverse matrix exists is also called an invertible matrix.
AB-1 B-1 A-1. Let us check more about each of the properties of matrices. The inverse of A is A-1 only when AA-1 A-1A I.
Properties of Matrix. This leads to an easy way of specifying the sparse patterns of the inverse covariance matrices and also results in. Properties of Inverse Matrices.
Let A be a square n by n matrix over a field K eg the field R of real numbers. If A has an inverse matrix then there is. Using properties of matrix all the algebraic operations such as.
We have learnt about the inverse matrix its properties and its examples. The one-to-one and onto properties 98 11. Let A be an n n matrix.
Any square matrix A over a field R. Properties The invertible matrix theorem.

Inverse Matrices And Their Properties Youtube
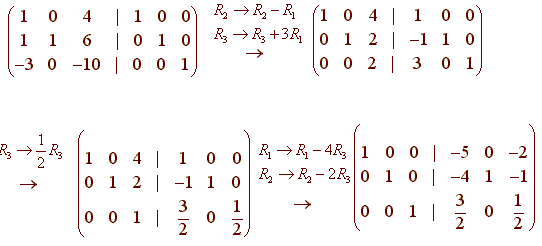


No comments for "Matrix Inverse Properties"
Post a Comment